TOC
双线插值是什么?
图像处理中,有时我们需要放大图片,比如原来图片宽高是300*300px,如果要在500*500的屏幕上展示,这时一种方法就是把图片直接拉大到500*500,但会发现图像变得模糊了,有没有什么办法可以放大图像而又不会让图像过于模糊呢?
答案是有的,就是向图像中插入一些像素,使得图片被填充到500*500px,这时图像的分辨率不会降低,即不会模糊。
那向原图像中插入的像素值是多少合适呢?肯定不是固定值,如果插入固定值,比如插入0,那图像就会多很多黑点,像有污点,不适合。
比较合适的插入像素值为其周围邻近点的值,这样填充出来的图像就与原图很像,分辨率还不会降低。
单线插值
在了解双线插值之前,我们先来了解什么是单线插值。
单线插值是在两个已知的点中插入一个新值。
比如已知A点坐标为(x0,y0)和C点坐标(x1,y1),AC两点连线,插入的坐标点B(x,y),点C在AC连线上,根据斜率相同(或根据相似三角形)有
(y-y0)/(x-x0) = (y1-y0)/(x1-x0)
这个式子可以化为 y-y0 = [ (y1-y0) * (x-x0) ] / (x1-x0)
y = {[ (y1-y0) * (x-x0) ] / (x1-x0) } + y0
y = { [ y1x - y1x0 - y0x + y0x0) ] / (x1-x0) }
y = { [ y1x - y1x0 - y0x + y0x0 + y0x1 - y0x0 ] / (x1-x0) }
y = { [ y1x - y1x0 - y0x + y0x1] / (x1-x0) }
y = [y1(x - x0) + y0 (x1 - x) ] / (x1-x0)
y (x1-x0) = y0 (x1 - x) + y1(x - x0)
最后的公式可以描述为:
B点的高 * AC两点的宽 = (A点的高 * BC两点的宽) + (C点的高 * AC两点的宽)
如下图所示:
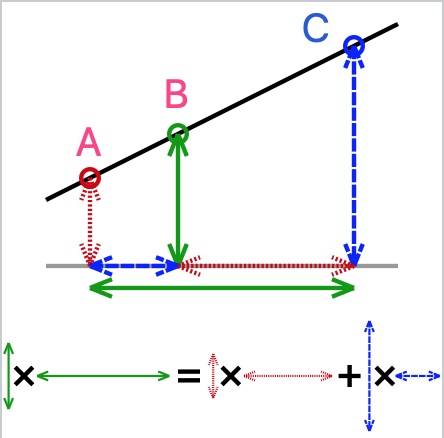
双线插值
理解了单线插值,现在我们可以来理解下双线插值。
先来理下我们知道的信息,我们知道要缩放的目标图像的尺寸,假如目标图像是600*800,原图像尺寸是300*400,缩放比例是scale_w=300/600=0.5(宽缩放比例); scale_h=400/800=0.5(高度缩放比例), 对于目标图像的任一个点坐标(x,y),我们可以通过x*scale_w得到源图像对应src_x坐标,同理得y*scale_h=src_y,这个点是原图像的点。
有原图像坐标值后,取其左上,左下,右上,右下可以得到四个点,即双线插值用到的四个点:Q11 = (x1, y1), Q12 = (x1, y2), Q21 = (x2, y1), and Q22 = (x2, y2),这四个点是已知信息。
如下图所示:
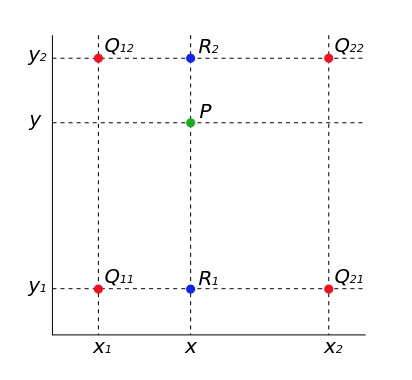
先对x轴做线性插值,根据单线插值:
f(x,y1) = f(R1) = [(x2 - x) / (x2 - x1) ] * f(Q11) + [(x - x1) / (x2 - x1) ] * f(Q21)
原理是R点离哪个点近,该点对R点的影响更大。这里需要注意是f(Q11)是指Q11点的实际值,对图像来说就是像素值(0-255),而不再是Q11点的坐标。
同理得
f(x,y2) = f(R2) = [(x2 - x) / (x2 - x1) ] * f(Q12) + [(x - x1) / (x2 - x1) ] * f(Q22)
得到R1和R2的值后,这时R1与R2连线,可计算P点的值:
f(x,y) = f(P) = [(y2 - y) / (y2 - y1) ] * f(R1) + [(y - y1) / (y2 - y1) ] * f(R2)
到这一步,P点的值就计算出来了。
在实际编写双线插值的算法中,P点的x和y是已知值,再通过上面公式即可计算出P点的值。
附维基百科里以图片的形式来表示双线插值。
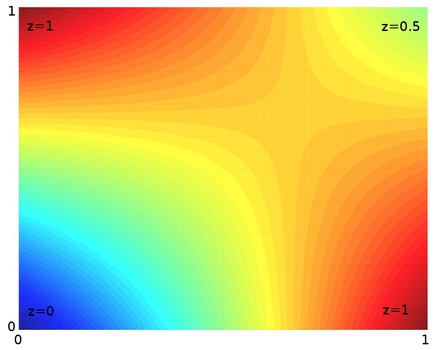
REFERENCES: Linear interpolation
「点个赞」
点个赞
使用微信扫描二维码完成支付
